| Nosotros have seen many graphs that are expressed as single equations and are continuous over a domain of the Existent numbers. We accept likewise seen the "detached" functions which are comprised of separate unconnected "points". There are also graphs that are defined by "different equations" over unlike sections of the graphs. These graphs may be continuous, or they may contain "breaks". Because these graphs tend to look like "pieces" glued together to form a graph, they are referred to as "piecewise" functions (piecewise defined functions), or "dissever-definition" functions. 
A piecewise defined function is a function defined by at least 2 equations ("pieces"), each of which applies to a different role of the domain. Piecewise defined functions can accept on a variety of forms. Their "pieces" may be all linear, or a combination of functional forms (such as constant, linear, quadratic, cubic, square root, cube root, exponential, etc.). Due to this diversity, there is no "parent function" for piecewise defined functions. The case below will incorporate linear, quadratic and constant "pieces". | 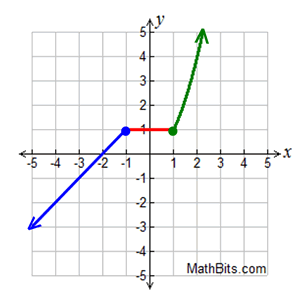
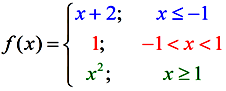
Notice that each "slice" of the function has a specific constraint.
| Description:
Detect that the "changes" focus around the x-values of 1 and -1.
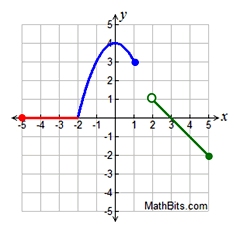
♦ Hint: When graphing, focus on where the changes in the graph occur. From ten-values of -∞ to -1, the graph is a straight line. From x-values of -one to 1, the graph is constant. From 10-values 1 to ∞, the graph is quadratic (part of a parabola). | The piecewise function shown in this instance is continuous (there are no "gaps" or "breaks" in the plotting). In this instance, the domain is all Reals since all x-values have a plotted value.
|  | For assist with piecewise defined functions on your calculator,
Click Here! | |
Withal dislocated about what is happening in these piecewise defined functions?
Attempt taking a look at each section as a "divide" graph, and grab your scissors!
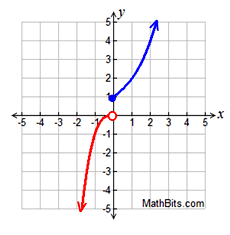
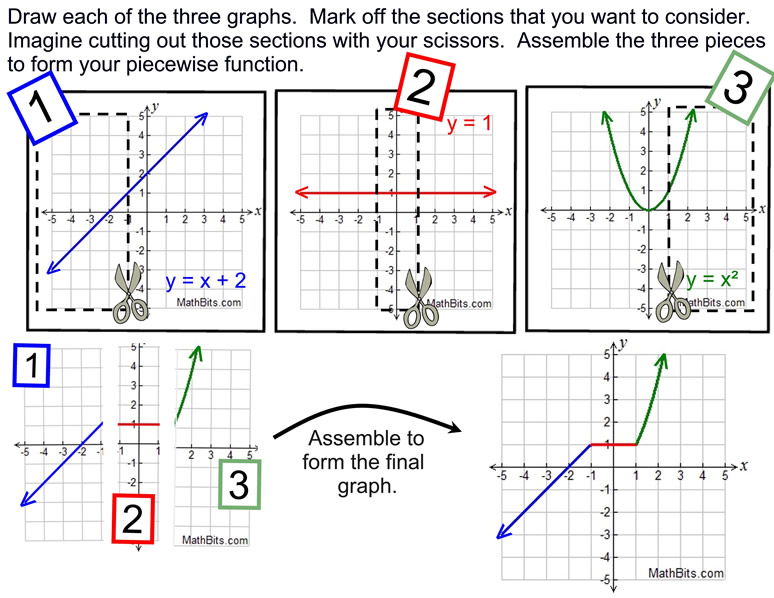  Piecewise defined functions may be continuous (equally seen in the case to a higher place), or they may be discontinuous (having breaks, jumps, or holes as seen in the examples below). Other Examples of Piecewise Defined Functions:

One of the most recognized piecewise defined functions is the absolute value function. | 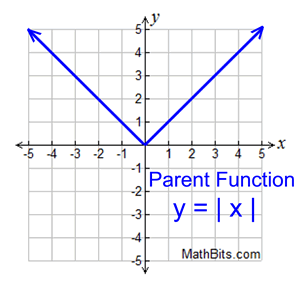 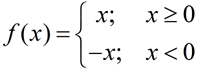 | Features (of parent function):
• Domain : All Reals (-∞,∞)
Unless domain is altered.
• Range: [0,∞) • increasing (0, ∞)
• decreasing (-∞,0) • positive (-∞, 0) U (0, -∞) • accented/relative min is 0
• no accented max (graph → ∞) • end behavior
f (x) → +∞, equally ten → +∞
f (x) → +∞, as ten → -∞ | Symmetric:
about x = 0
unless domain is altered
ten-intercept:
intersects x-centrality at (0, 0)
unless domain is altered y-intercept:
intersects y-centrality at (0, 0)
unless domain is altered
Vertex:
the betoken (0,0)
unless domain is altered
|
| Range: When finding the range of an absolute value role, discover the vertex (the turning point). • If the graph opens upwards, the range will be greater than or equal to the y-coordinates of the vertex. • If the graph opens downward, the range will be less than or equal to the y-coordinate of the vertex. | Average charge per unit of change:
is constant on each directly line section (ray) of the graph. | |  | For help with absolute value graphs on your calculator,
Click Hither! | | | Accented Value Part - Transformation Examples: | 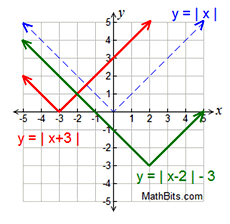
Translations | 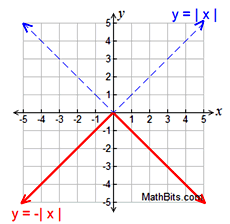
Reflection | 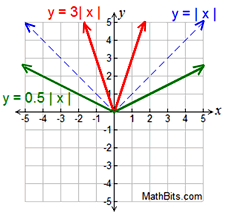
Vertical Stretch/Compress |

A step part (or staircase function) is a piecewise function containing all abiding "pieces". The constant pieces are observed beyond the adjacent intervals of the function, as they change value from one interval to the next. A step role is discontinuous (non continuous). You cannot draw a step office without removing your pencil from your paper. | 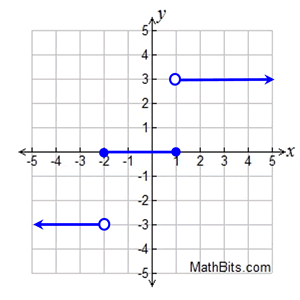 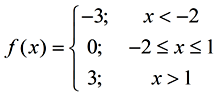 | Features (of step functions):
• utilize open circles and/or closed circles on the graph
open = point not on graph; closed = point is on graph • horizontal "pieces" • discontinuous (cannot exist drawn without removing your pencil from the newspaper) | • notice the resemblance to a set of steps • may, or may not, be a office. Check with the vertical line exam.
This example is a office. | 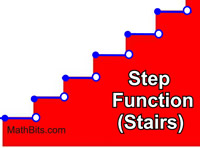 | | 1 of the most famous pace functions is the Greatest Integer Function.
The greatest integer function returns the largest integer less than or equal to x, for all existent numbers x. In essence, the greatest integer function rounds down a real number to the nearest integer. For example: [2] = ii; [1.5] = 1; [-3.one] = -four; [-6.9] = -7 | Greatest Integer Function: 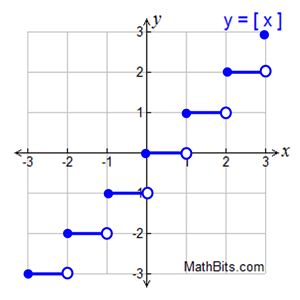 | Features - the Greatest Integer Part:
• the intervals on the greatest integer role can exist expressed as [due north, north+1). The value of the function on these intervals volition be north. The function is constant in each interval. • you may see some texts using the notation y = [[x]] (double brackets). • information technology may likewise be referred to equally the "floor" function and written every bit 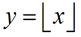 . .
This site will use the single bracket annotation y = [ten].
| |  | For assistance with greatest integer functions on your calculator,
Click Here! | | |
More examples of Step Functions:  Note: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is non considered "fair use" for educators. Please read the "Terms of Apply". |


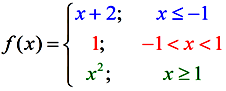


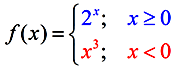


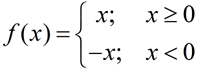





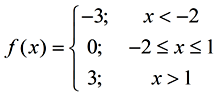


0 Response to "Absolute Value Greatest Integer and Piecewise Function Review Worksheet Answer"
Post a Comment